Embark on an enlightening journey as we delve into the fascinating world of significant figures, where precision and accuracy dance together. Join us as we unveil the secrets behind “how many sig figs in 8000,” a question that has puzzled countless minds.

In this comprehensive guide, we’ll navigate the intricacies of determining significant figures, unraveling the rules that govern their presence, and exploring their profound implications in scientific calculations. Prepare to be captivated as we illuminate the significance of every digit, unlocking the mysteries that lie within the realm of measurements.

Understanding Significant Figures

Significant figures, also known as significant digits, are the digits in a number that are known with certainty, plus one uncertain digit. They provide information about the precision and accuracy of a measurement.

Precision refers to the closeness of a measurement to its true value, while accuracy refers to how close a measurement is to the accepted value. A measurement can be precise but not accurate, or accurate but not precise.

Examples of Numbers with Different Significant Figures

• 100 has 3 significant figures (1, 0, and 0).
• 100.0 has 4 significant figures (1, 0, 0, and 0).
• 0.001 has 1 significant figure (1).
• 123.45 has 5 significant figures (1, 2, 3, 4, and 5).
• 1.234 x 10^3 has 4 significant figures (1, 2, 3, and 4).

Determining Significant Figures in 8000: How Many Sig Figs In 8000

In the number 8000, the significant figures are 8 and 0. The first non-zero digit, 8, is always significant. The zeros following the 8 are significant because they are between non-zero digits. Therefore, the number 8000 has 2 significant figures.

Rules for Determining Significant Figures

The rules for determining significant figures in numbers are as follows:

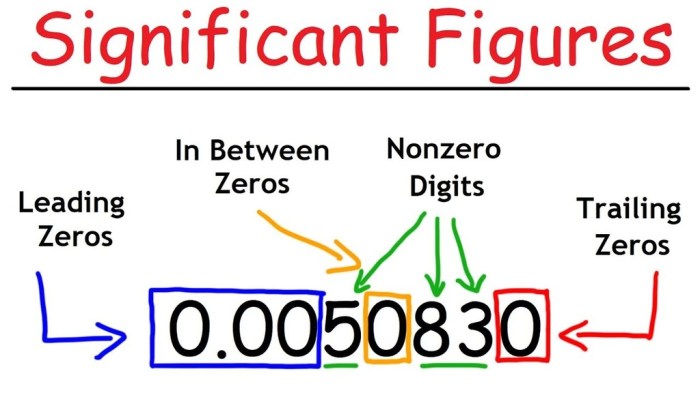
• All non-zero digits are significant.
• Zeros between non-zero digits are significant.
• Trailing zeros after the decimal point are significant.
• Leading zeros are not significant.

Examples and Applications

Understanding significant figures is crucial in various fields, including science and engineering. Here are some examples and applications that highlight their importance:

Examples of Numbers with Different Significant Figures

Consider the following numbers:

• 100 (2 significant figures)
• 100.0 (3 significant figures)
• 0.001 (1 significant figure)
• 1.234 (4 significant figures)
• 1.2340 (5 significant figures)

These examples demonstrate how the number of significant figures conveys different levels of precision. 100 has only 2 significant figures, indicating that it is an approximate value, while 1.2340 has 5 significant figures, suggesting a more precise measurement.

Importance of Significant Figures in Scientific Calculations

Significant figures are essential in scientific calculations to maintain accuracy. When multiplying or dividing numbers, the result should be reported with the same number of significant figures as the number with the fewest significant figures involved in the calculation.

8000 has two significant figures, but if you’re looking for a more in-depth review of laboratory techniques, check out the csun bus 302 lab review . Returning to our original topic, the number of significant figures in 8000 is still two, indicating the level of precision in the measurement.

For example, if we multiply 1.23 (3 significant figures) by 4.5 (2 significant figures), the result should be reported as 5.6 (2 significant figures), as the number with the fewest significant figures (4.5) determines the precision of the final answer.

How Significant Figures Affect the Accuracy of Measurements, How many sig figs in 8000

Significant figures indicate the accuracy of a measurement. A measurement with more significant figures is generally more accurate than one with fewer significant figures.

For instance, if we measure the length of an object and report it as 10.0 cm (3 significant figures), it implies that the measurement is accurate to the nearest 0.1 cm. On the other hand, if we report it as 10 cm (2 significant figures), it indicates that the measurement is only accurate to the nearest 1 cm.

Extensions

In addition to the basic rules for determining significant figures, there are several extensions that can help you apply these rules more effectively.

Trailing Zeros

Trailing zeros are zeros that appear at the end of a number. They can be either significant or insignificant, depending on their position.

• Significant trailing zerosare those that appear after a decimal point or after a non-zero digit.
• Insignificant trailing zerosare those that appear at the end of a whole number.

For example, in the number 8000, the trailing zero is insignificant because it appears at the end of a whole number. However, in the number 8000.0, the trailing zero is significant because it appears after a decimal point.

Scientific Notation

Scientific notation is a way of expressing very large or very small numbers in a more compact form. It is written as a number between 1 and 10 multiplied by a power of 10.

When a number is written in scientific notation, the number of significant figures is determined by the number of digits in the coefficient, not including the leading 1.

For example, the number 8000 can be written in scientific notation as 8.000 x 10 ³. This number has three significant figures.

Operations with Numbers That Have Different Significant Figures

When performing operations with numbers that have different significant figures, the answer should be reported to the least number of significant figures of the numbers being added, subtracted, multiplied, or divided.

• Addition and Subtraction:The answer should be reported to the least number of decimal places of the numbers being added or subtracted.
• Multiplication and Division:The answer should be reported to the least number of significant figures of the numbers being multiplied or divided.

For example, if you add the numbers 8000 and 200, the answer should be reported to the least number of decimal places, which is 0. Therefore, the answer is 8200.

If you multiply the numbers 8000 and 200, the answer should be reported to the least number of significant figures, which is 3. Therefore, the answer is 1.60 x 10 ⁶.

Answers to Common Questions

What is the significance of significant figures?

Significant figures indicate the reliability of a measurement, reflecting the number of digits known with certainty and one estimated digit.

How do I determine the significant figures in 8000?

8000 has two significant figures: 8 and 0. The first non-zero digit (8) and all subsequent zeros are significant.

Why are trailing zeros significant in 8000?

Trailing zeros in 8000 (e.g., 8000.00) indicate the precision of the measurement, specifying that the measurement was made to the nearest hundredth.