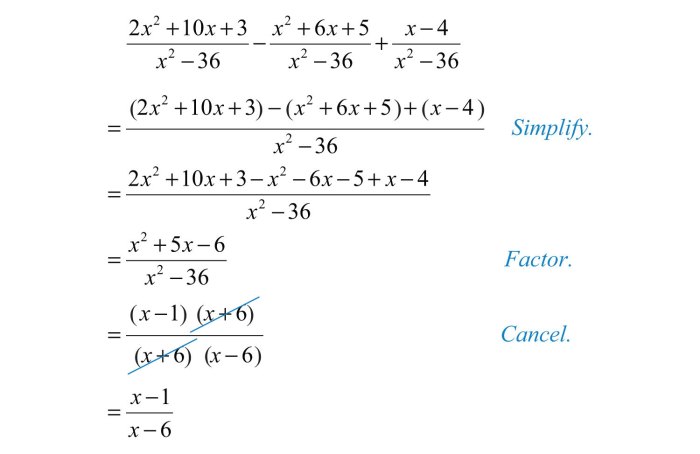Embark on a mathematical adventure with our engaging “Adding and Subtracting Rational Expressions Quiz”! This quiz will guide you through the intricacies of rational expressions, empowering you to confidently tackle even the most complex algebraic challenges.

Delve into the fascinating world of rational expressions, where fractions take center stage. Understand their mathematical representation and significance in mathematical operations. Learn the art of combining and subtracting these expressions, mastering the techniques for both same and different denominators.

Adding and Subtracting Rational Expressions

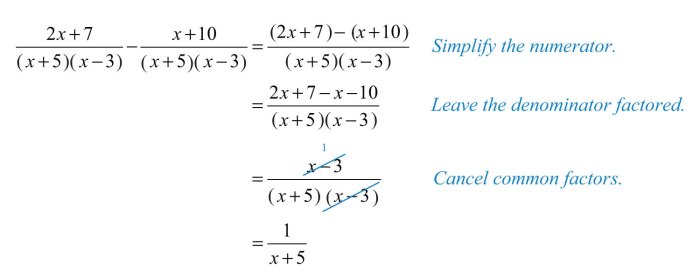
Rational expressions are mathematical expressions that involve fractions of polynomials. They are used to represent complex algebraic expressions and have applications in various fields of mathematics, including algebra, calculus, and physics.

Adding and subtracting rational expressions is a fundamental operation in algebra that requires an understanding of their mathematical representation and the rules of algebraic operations. This article provides a comprehensive overview of adding and subtracting rational expressions, including step-by-step guides and illustrative examples.

1. Overview of Rational Expressions

A rational expression is a fraction of two polynomials, represented as p(x)/q(x), where p(x) and q(x) are polynomials and q(x) is not equal to zero. Rational expressions are used to represent algebraic expressions that cannot be simplified into a single term.

Understanding rational expressions is crucial for performing algebraic operations, such as addition, subtraction, multiplication, and division. Rational expressions find applications in solving equations, simplifying complex algebraic expressions, and modeling real-world problems.

2. Adding Rational Expressions with the Same Denominator, Adding and subtracting rational expressions quiz

To add rational expressions with the same denominator, add the numerators and keep the denominator the same. For example, to add (2x + 3)/(x – 1) and (x – 5)/(x – 1), we have:

(2x + 3)/(x – 1) + (x – 5)/(x – 1) = [(2x + 3) + (x – 5)]/(x – 1) = (3x – 2)/(x – 1)

This is because the denominators are the same, so we can simply add the numerators and keep the denominator.

3. Adding Rational Expressions with Different Denominators

To add rational expressions with different denominators, we need to find a common denominator. The Least Common Multiple (LCM) of the denominators is the smallest polynomial that is divisible by both denominators. For example, to add (2x + 3)/(x – 1) and (x – 5)/(x + 2), we have:

LCM(x – 1, x + 2) = (x – 1)(x + 2)

Then, we can rewrite the expressions with the common denominator:

(2x + 3)/(x – 1) = [(2x + 3)(x + 2)]/[(x – 1)(x + 2)] = (2x^2 + 7x + 6)/(x^2 + x – 2)

(x – 5)/(x + 2) = [(x – 5)(x – 1)]/[(x – 1)(x + 2)] = (x^2 – 6x + 5)/(x^2 + x – 2)

Now, we can add the expressions with the same denominator:

(2x^2 + 7x + 6)/(x^2 + x – 2) + (x^2 – 6x + 5)/(x^2 + x – 2) = (3x^2 + x + 11)/(x^2 + x – 2)

4. Subtracting Rational Expressions with the Same Denominator

To subtract rational expressions with the same denominator, subtract the numerators and keep the denominator the same. For example, to subtract (x – 5)/(x + 2) from (2x + 3)/(x + 2), we have:

(2x + 3)/(x + 2) – (x – 5)/(x + 2) = [(2x + 3) – (x – 5)]/(x + 2) = (x + 8)/(x + 2)

This is because the denominators are the same, so we can simply subtract the numerators and keep the denominator.

5. Subtracting Rational Expressions with Different Denominators

To subtract rational expressions with different denominators, we need to find a common denominator. The Least Common Multiple (LCM) of the denominators is the smallest polynomial that is divisible by both denominators. For example, to subtract (x – 5)/(x – 1) from (2x + 3)/(x + 2), we have:

LCM(x – 1, x + 2) = (x – 1)(x + 2)

Then, we can rewrite the expressions with the common denominator:

(x – 5)/(x – 1) = [(x – 5)(x + 2)]/[(x – 1)(x + 2)] = (x^2 – 6x + 5)/(x^2 + x – 2)

(2x + 3)/(x + 2) = [(2x + 3)(x – 1)]/[(x – 1)(x + 2)] = (2x^2 + x + 3)/(x^2 + x – 2)

Now, we can subtract the expressions with the same denominator:

(2x^2 + x + 3)/(x^2 + x – 2) – (x^2 – 6x + 5)/(x^2 + x – 2) = (x^2 + 7x – 2)/(x^2 + x – 2)

6. Quiz on Adding and Subtracting Rational Expressions

1. Add the rational expressions (x + 2)/(x
   • 3) and (x
   • 1)/(x
   • 3).
2. Subtract the rational expression (2x + 1)/(x + 2) from (3x
   

   2)/(x + 2).

3. Find the LCM of the denominators (x
   

   2) and (x + 3).

4. Add the rational expressions (x
   • 5)/(x
   • 2) and (2x + 3)/(x + 3).
5. Subtract the rational expression (x + 2)/(x
   • 1) from (3x
   • 5)/(x
   • 1).

Answer Key:

1. (2x + 1)/(x
   

   3)

2. (x
   

   3)/(x + 2)

3. (x^2 + x
   

   6)

4. (4x^2
   • 7x
   • 11)/(x^2 + x
   • 6)
5. (2x
   • 7)/(x
   • 1)

FAQ: Adding And Subtracting Rational Expressions Quiz

What is a rational expression?

A rational expression is a fraction where both the numerator and denominator are polynomials.

How do you add rational expressions with the same denominator?

Add the numerators and keep the denominator the same.

How do you add rational expressions with different denominators?

Find the least common multiple (LCM) of the denominators, and then multiply each fraction by an appropriate factor so that all the denominators are the same.