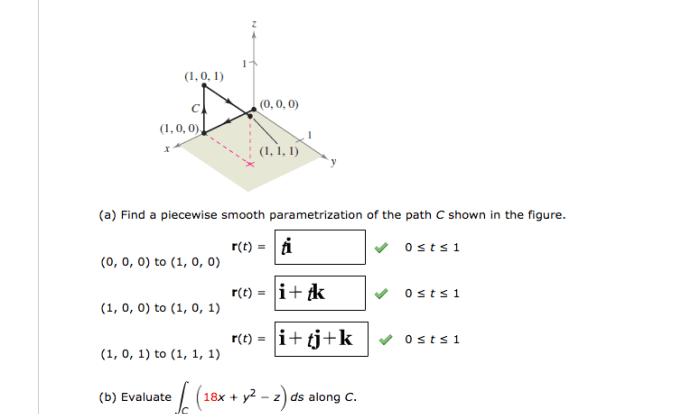
Unit 11 test volume and surface area – Unit 11 Test: Volume and Surface Area Explored takes us on an in-depth journey into these fundamental geometric concepts. This examination delves into the intricacies of calculating volume and surface area, their interrelationships, and their practical applications across diverse fields, providing a comprehensive understanding of these essential mathematical tools.

Throughout this exploration, we will uncover the formulas and techniques for determining the volume of common shapes, such as cubes, spheres, and cones. We will also investigate the surface area of these shapes, examining the steps involved in calculating their surface area and exploring how these concepts are applied in real-world scenarios.

Volume and Surface Area Concepts

Volume is a measure of the three-dimensional space occupied by an object, while surface area is a measure of the total area of its surfaces. These concepts are fundamental in various fields, including geometry, engineering, and biology.

Volume is typically measured in cubic units (e.g., cubic centimeters, cubic meters), while surface area is measured in square units (e.g., square centimeters, square meters).

The relationship between volume and surface area is important in many applications. For example, in heat transfer, the surface area of an object affects the rate at which it loses or gains heat.

Volume of Common Shapes

The volume of a shape can be calculated using specific formulas. Here are some common shapes and their volume formulas:

• Cube: V = a³, where ais the length of an edge
• Sphere: V = (4/3)πr³, where ris the radius
• Cone: V = (1/3)πr²h , where ris the radius of the base and his the height
• Cylinder: V = πr²h , where ris the radius of the base and his the height

These formulas can be applied to solve problems involving the volume of objects.

Surface Area of Common Shapes

The surface area of a shape can be calculated using specific formulas. Here are some common shapes and their surface area formulas:

• Cube: A = 6a², where ais the length of an edge
• Sphere: A = 4πr², where ris the radius
• Cone: A = πr²+ πrs , where ris the radius of the base, sis the slant height
• Cylinder: A = 2πrh + 2πr², where ris the radius of the base and his the height

These formulas can be applied to solve problems involving the surface area of objects.

Applications of Volume and Surface Area: Unit 11 Test Volume And Surface Area

Volume and surface area have numerous practical applications in various fields:

• Engineering: Designing structures, calculating fluid flow, and optimizing heat transfer systems.
• Architecture: Determining the volume and surface area of buildings, optimizing energy efficiency, and ensuring structural stability.
• Biology: Calculating the volume of cells and tissues, studying surface-to-volume ratios, and understanding diffusion processes.
• Packaging: Optimizing the volume and surface area of containers to minimize material usage and maximize product protection.
• Manufacturing: Calculating the volume of materials needed for production, optimizing surface area for coating or painting processes.

Detailed FAQs

What is the relationship between volume and surface area?

Volume measures the amount of three-dimensional space occupied by an object, while surface area measures the total area of its surfaces. In general, objects with larger volumes tend to have larger surface areas, although this relationship is not always proportional.

How are volume and surface area used in real-world applications?

Volume and surface area are essential concepts in various fields, including engineering, architecture, and biology. For example, engineers use volume to calculate the capacity of containers and surface area to determine the amount of material needed for construction. Architects consider volume and surface area when designing buildings to optimize space and energy efficiency.

In biology, volume and surface area are used to study the size and shape of cells and organisms.