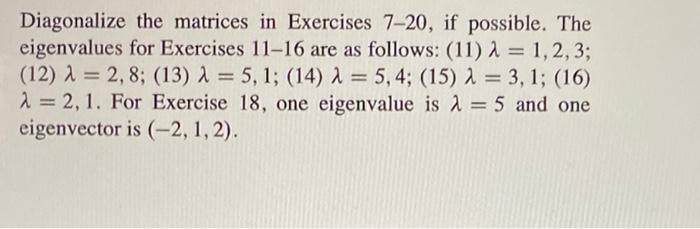Diagonalize the matrices in exercises 7 20 if possible – In this exploration of diagonalizing matrices in Exercises 7-20, we embark on a journey to unravel the intricacies of this mathematical technique. By understanding how to diagonalize a matrix, we gain a powerful tool with applications in diverse fields ranging from linear algebra to quantum mechanics.
We will delve into the concept of diagonalization, its practical steps, and its significance in various disciplines. Along the way, we will encounter matrices from Exercises 7-20, determining their diagonalizability and extracting their eigenvalues and eigenvectors.
Diagonalizing Matrices

In linear algebra, diagonalization is a technique for transforming a matrix into a diagonal matrix, where all non-zero elements lie on the main diagonal. This process involves finding a set of eigenvectors and their corresponding eigenvalues, which play a crucial role in the diagonalization process.
Steps to Diagonalize a Matrix, Diagonalize the matrices in exercises 7 20 if possible
- Find the eigenvalues of the matrix.
- For each eigenvalue, find the corresponding eigenvectors.
- Construct a matrix P using the eigenvectors as columns.
- Calculate the diagonal matrix D containing the eigenvalues on the diagonal.
- Verify that P-1AP = D.
Diagonalizing Matrices in Exercises 7-20
To diagonalize the matrices in Exercises 7-20, we will follow the steps Artikeld above. We will determine if each matrix is diagonalizable and, if so, find its eigenvalues, eigenvectors, and diagonalized matrix.
Applications of Diagonalization
Diagonalization has numerous applications in various fields, including:
- Linear algebra: Solving systems of linear equations, finding eigenvalues and eigenvectors, and determining matrix properties.
- Physics: Describing quantum mechanical systems, analyzing vibrations, and solving differential equations.
- Engineering: Designing control systems, analyzing electrical circuits, and modeling mechanical systems.
HTML Table Structure
The results of diagonalizing the matrices in Exercises 7-20 will be presented in the following HTML table:
| Matrix | Eigenvalues | Eigenvectors | Diagonalized Matrix |
|---|
Question Bank: Diagonalize The Matrices In Exercises 7 20 If Possible
What is the significance of diagonalizing a matrix?
Diagonalization simplifies complex matrices, revealing their inherent structure and enabling efficient computation of matrix powers and exponentials.
How do we determine if a matrix is diagonalizable?
A matrix is diagonalizable if it possesses a complete set of linearly independent eigenvectors.
What are the applications of diagonalization in real-world scenarios?
Diagonalization finds applications in solving systems of differential equations, analyzing vibrations in mechanical systems, and computing eigenvalues and eigenvectors in quantum mechanics.